という話が届けられました。内積は、高校ではベクトルの演算の1つとして習います。しかし、大学で学ぶ線形代数の中では、内積という演算がじつは、空間を規定する重要な写像であり、ベクトルはそこで定義されたものに過ぎないという事がわかります(「ベクトル空間は内積空間の一部である」という)。多分そこで、概念の拡張が難しいんだと思います。
そこで、ベクトルのスカラー積としての内積からそれを拡張して、できるだけそこからかけ離れないようなイメージで解説してみます。だいぶ解説が長く、高校の範囲とかぶる部分も多いので、読み飛ばせるように小分けしてあります。
余裕があれば、外積とテンソルについても触れたいと思います。
u・v = ||u|| ||v|| cosθ
と定義されます。大きさを二重棒線で表わしたのは、あとで説明する「ノルム」の表記に合わせているためです。成分表示するには、余弦定理より、
u・v = (1/2)(||u||^2 + ||v||^2 - ||v - u||^2)
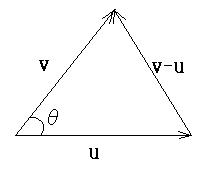
と書けて、これに
u = (u1, u2, u3), v = (v1, v2, v3)
を代入すると、
u・v = u1v1 + u2v2 + u3v3
ただしここで注意しなければならないのは、成分表示の方は、余弦定理が成り立たないと成り立たない、つまり、ユークリッド空間(Euclid place)でのみ成り立つということです。(この事は後ほど述べます。)
「物体をある力 F に逆らって変位 s を与える時、なされた仕事は
Fs cosθである」
でした。例えば、重力場に逆らって質量 m の物体を持ち上げる事を考えると、鉛直上向きに s だけ変位を与えるとすれば、そのときになす仕事は単純に、mgsです。しかし、鉛直上向きに対してθだけ斜めに持ち上げると、変位は s ですが、
「重力に逆らう方向は鉛直上向きであり、逆らう距離は s cosθである」
ので、なされた仕事は mg(s cosθ)となることは教科書に書いてある通りです。
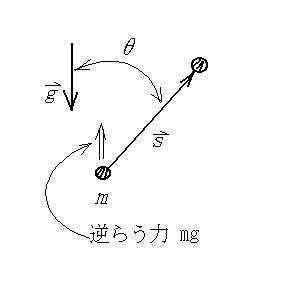
θが直角のとき、すなわち真横に移動する時は、重力の方向に逆らう成分は無いので仕事は0です。また、重力自体は持ち上げる力と真反対に働くので、負の仕事をすることになります。
これは変位にスポットを当てた言い方ですが、力が傾いていると考えても良いわけで、
「かかる力は mg だが、変位に対してθだけ傾いているので、逆らうべき力はmg cosθである」
という言い方も出来ます。
すなわち力と変位は数学的に同等で、仕事は変位と力の内積 F・s と書けます。ここからベクトルの内積とは、
「2つのベクトルの何らかの相乗効果を表すもの」
と言うことが出来るでしょう。なおこの場合は、変位も力も一方向で保存している場合についての話ですが、それ以外の場合も、線積分 ∫F・dsの中身はベクトルの内積なので、本質的には変わりません。
余談ですが、仕事と言うのはスカラー量ですが、このように方向性を持っているので混乱しがちなのではないでしょうか。これは、すなわち仕事がベクトルの内積である事からで、仕事の結果としての仕事量はスカラー量ですが、仕事そのものの過程は方向性があることを意味しています。
これは現実の感覚とも当てはまります。すなわち、いくら作業をしても、その進む方向が目的の方向を向いていなければ、仕事の結果が現われないわけです。上の例では、いくら変位を与えても、重力に逆らって持ち上げなければ仕事として加算されないのです。書類を渡されてデータの整理を頼まれ、その書類を全て紙飛行機にしたとすれば、紙飛行機にしたという作業はしても、データが整理されているという仕事の結果は出ないですよね。
ベクトル u, v が直交 ⇔ 内積 u・v = 0
でした。すなわち cosθ= 0 ということなのですが、これは画期的です。例えば成分で与えられたベクトルの直交を示すには、平面であれば図形的な手法で示す事は容易ですが、立体になるとその位置関係を把握するのは厄介です。しかし、内積が0である事と同値であれば、数式でそれを示せば良いだけの話です。
また何より、内積による表現は普遍であるので、拡張性が高いと言うメリットがあります。すなわち、直交を数式上で示せるので、図形的に表現が不可能な n 次元ユークリッド空間においても、直交が定義できる事になります。
さらに、内積を始めに述べた方法以外で定義し、内積 u・v それ自体をある意味のある値とする事が出来れば、ユークリッド空間以外でも内積 = 0で直交が定義できます。(その定義は後ほど述べます。)
例えば極端に、関数においても「直交」が定義できます。その時の内積の定義も同様に、2つの関数を f, g とすると、
<f, g> = ∫f・g
とされます。
∫[-π;π] {sinθ・cosθdθ}= 0
の例は有名だと思いますが、これは、sin と cos が直交している事を示しています。(これは位相差がπ/2 なので、図形的意味のアナロジーが利くでしょう。)ちなみに、区分的に滑らかな任意の周期関数はフーリェ級数で正弦波の重ね合わせとして表す事ができ、三角関数の直交性を利用して関数の直交関係を調べる事が出来るのは、納得いくと思います。
定義は、
||u|| = <u, u>^(1/2) (= (||u|| ||u|| cos 0)^(1/2))
です。何故「ノルム」という呼び方をするのかは良く分かりません。英語の"norm"は「規定」という意味で、よく言われる「ノルマ」と同じものです。「大きさ」というと形あるものにしか定義できませんが、内積によって形の定義できないようなものについても、同じ手続きで「大きさ」にあたるものを測る規準を与えるという意味で、「ノルム」と呼んでいるんだと思います。
大きさが定義できたならば「距離」も定義できるわけで、2つのベクトルの距離は、
d (u, v) = ||u - v|| = <u - v, u - v>^(1/2)
と表されます。
「直交」「ノルム」を定義できれば、これらによって「正規直交基底」(基底ベクトル)というものを作り、任意のベクトルを基底の1次結合で書くことが出来るわけです。すなわち、内積によって「空間」を定義できた事になり、これを「内積空間」と言うわけです。内積空間は、基底の1次結合で任意の要素を表現できるので、「線形空間」です。
余談ですが、フーリエ級数も、関数空間における正規直交基底によって、関数を基底関数の1次結合で表したものと考える事が出来るのです。
そこで、内積は次のように一般化された形で定義されているのです(簡単のため、複素ベクトルを含んだユニタリー空間についての解説は省略)。
次のような写像が定義される線形空間を、内積空間という。
・<u, v> = <v, u> (交換則)
・<u + v, w> = <u, w> + <v, w> (分配則)
・<ku, v> = k<u, v> (線形性)
・<v, v>≧0 (非負性)
一見当たり前のような、演算について抽象的な定義しかされていないが、数学的な定義はこれだけです。
これだけではどういう内積でもとれてしまうではないか、と思われるかもしれないですが、その通りで、単に線形空間が与えられているだけでは、内積は一意に決まるものではないのです。
よって、内積空間という場合には、その内積の演算の中身を決定してやる必要があり、それはベクトル空間を与える時に、座標のとり方を決める事に相当します。当然内積のとり方によって、前に述べたノルムや直交条件も違ってきます。
その意味で、始めに述べた座標表示のユークリッド内積の座標表示
u・v = u1v1 + u2v2 + u3v3
は一般的ではないのです。例えばこれを、
u・v = 3 u1v1 + 2 u2v2 + 5 u3v3
としても、先に述べた内積を定義する4つの性質を満たす事を確認してみてください。
こうして内積の演算を定義する事により、
距離・・・||u - v|| = <u - v, u - v>^(1/2)
角度・・・cosθ= <u, v> / [||u|| ||v||]
を規定し、空間が内積で決定できるようになるのです。そして、この拡張はユークリッド空間においてではなく、図示する事の出来ない(図形的意味を持たない)空間へ拡張出来るようになった事が重要です。
「内積で定義されたノルムに関して完備な(空間 H 上で取れる、ノルムに関する全てのコーシー列の極限が、 H 上の点に収束する)内積空間」
のことを「ヒルベルト空間」といいます。完備性を要求しない、ただの内積空間は「プレ - ヒルベルト (pre -)空間」と言います。この辺のことは良く分からなくても良いです。時々細かいことを指摘されるので書いてるだけですが、興味があればこの手の教科書はいくらでも出てますし、物理にとってそれほど重要な問題ではないと思われます。)
「ヒルベルト空間」というのは「関数空間」の1つですが、ユークリッド空間を無限次元に拡張したものであると述べられています。この辺のイメージを説明します。
まず平面(2次元)のベクトル空間の場合、「2つの一次独立なベクトル」 u, v をとると、 「u, v の存在する平面上全てのベクトル」を、
s u + t v (s, t をスカラーとして)
の形で表せます。
立体(3次元)だったら3つの1次独立なベクトル、そして n 次元だったら n 個の一次独立なベクトルで表す事が出来ます。
次に、多項式の場合を考えます。例えば x についての2次式
p = a0 + a1 x + a2 x^2, q = b0 + b1 x + b2 x^2
の和は、 p + q = (a0 + b0) + (a1 + b1) x + (a2 + b2) x^2
です。中学生も知っている至極当たり前の事なのですが、ここで何がいえるかというと、
「定数項、x の項、x^2 の項がそれぞれ1次独立である」
ということです。すなわち、この多項式から、
(a0, a1, a2), (b0, b1, b2)
という3次元ベクトルを抽出して計算を定義できるのです。ということは、
「2次多項式空間は、3次元ベクトル空間である」
そして、
「n 次多項式空間は、n + 1 次元ベクトル空間である」
と言えます。
なお、ここで内積は、
<p, q> = a0 b0 + a1 b1 + a2 b2
のように定義する事が出来ます。
ところで、いきなり「多項式がベクトルだ」と言われてもピンと来ないかもしれませんが、それはベクトルを図形的に捉えようとしているからであって、実は、線形代数学ではベクトルも、「和とスカラー倍の公理(要するに、「交換律」とか「結合律」とか「零元、逆元の存在」とか)」によって抽象的に定義されているので、先ほどの内積のように、定義された性質を持っていればそれはベクトルなのです。
しかし、この多項式の場合のように、順を追って重要な性質を抜き出して考えてみれば、なんら異質なものでは無い事がわかります。
さて、いよいよ「関数」への拡張です。
まず、数列 {fn}, {gn}
{fn} = f1, f2, ・・・,fn
{gn} = g1, g2, ・・・,gn
を考えます。この「数列」は、
n 次元ベクトル
とも言うことが出来ます。
これらの任意の"l"番目から"k"番目までの内積は、
<{fn}, {gn}>[k; l] = fk gk + f(k+1) g(k+1) +・・・+ fi gi +・・・+ fl gl
= Σ[k; l] fi gi
ここで、この数列{fn}, {gn} をそれぞれ、
「考えている区間で連続な関数 f ( t ), g ( t ) をそれぞれ、n 個の点でサンプリングしたもの」
と考えて、n →∞としてみましょう。
標本化されていた {fn}, {gn} はやがて連続になり(下図参照)、級数 Σ[k, l] fi gi は、
「無限小の幅で無限個の和、すなわち積分の定義であるリーマン和」
をとることになります。すなわち、n →∞の極限で
<{fn}, {gn}>[k; l] = Σ[k; l] fi gi(数列 {fn}, {gn} の内積)
→ <f ( t ), g ( t )>[a; b] =∫[a; b] f ( t ) g ( t ) dt(関数 f ( t ), g ( t ) の内積)
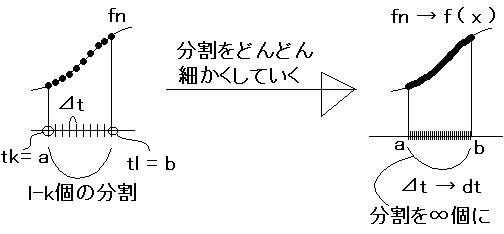
よって「関数空間」は、
「無限次元のベクトル空間」
すなわち、
「ユークリッド空間を無限次元に拡張したもの」
と言うことができるのです。ちなみに、この関数空間の任意の周期関数を直交基底で分解したものが
「フーリエ級数展開」
と考えられます。
すなわち「ヒルベルト空間」とは、
「一般の関数を無限次元のベクトルと考え、そこに内積を定義して、ノルムや向きを与えた空間」
と言えます。
ヒルベルト空間の他にも、三角不等式によって定義される「ノルム」から作られるノルム空間、それに完備性を持たせたバナッハ (Banach) 空間などがあります。内積で定義されたノルムは、当然ノルム空間の定義をみたしていて、ヒルベルト空間はバナッハ空間の部分空間と考えることも出来ます。