という話になって困ってしまいました。ラプラス変換の計算をすること自体はとても簡単なのですが、その意味をイメージした上で使っている人はあまりいないのではないでしょうか。
実際、工学の基礎数学であるラプラス変換については、多くの解説書も出まわっているのですが、ほとんどがその使い方に終始し、始めのほうに取ってつけたような定義の項目があるだけです。むしろそれが、初めて学ぶ人にとって混乱を招いてしまっているところもあると思います。
もちろん、これを厳密にやろうとすれば、数学の奥深い所に立ち入ることになりとても大変ですが、その「位置付け」のようなものを理解できれば、だいぶ見え方も違ってくると思います。
ここでは制御理論の基礎を中心に、複素関数論による導出まで立ち入らずに、関数変換の1つとしてその外観を捉え、フーリエ変換と比較することで、その意味に迫ってみたいと思います。
x ( t ) → [ F ] → y ( t )
というものです。
見ての通り、これは「関数」の考え方と何ら変わりはありませんね。関数は「数から数へ」という写像でしたが、変換はこれを関数でやろうというだけのことなのです。これを、「関数を引数に取る関数」という意味で、「汎関数 (functional)」ということがあります。
関数では「定義域」とか「連続性」とかいろいろ出てきましたが、変換でも初めの方に出てくる面倒くさい部分は、これと似たような事を調べているわけです。つまり、「変換前後の対応」とか、「どんな関数に成り立つか」といった、「写像」としての性質です。
一番馴染み深い関数の変換といえば、微積分だと思います。ちょっと話がそれてしまいますが、微積分の「写像」としての性質を見てみましょう。
微分を先ほどにならうと、微分の演算子を D として、
f ( x ) → [ D ] → f ' ( x )
となります。これは、
「ある関数」→「その変数領域での変化率」
という変換になっていると見る事が出来ます。速度、加速度の例もあるので、物理的意味は明らかでしょう。
この変換を行う為の条件は、
「関数が連続で、滑らかである」
という事でしたね。そしてこの変換は、
f ( x ) → [ D-1 ] → F ( x )
という逆変換も存在して、それが積分である事は云うまでも無いでしょう。
積分の場合の変換条件はちょっと複雑ですが、例えばリーマンの狭義積分だったら、
「関数が積分区間上で連続、または不連続点が有限個で、この区間で有界である(発散しない)」
ということです。広義積分であれば、積分区間を発散点にまで近付けたときの積分値が、有限な極限値を持てば良いわけです。
この辺の事は教科書にイヤというほど書いてありますが、ようは、
「積分できる関数を少しでも増やそう!」
「積分できる状況を少しでも増やそう!」
というスローガンがそこにはあるわけです。証明などは面倒くさいですが、
「どのような発想で、定義を拡張しているのか」
が分かれば十分だと思います。
実は、この微分・積分の条件等の話と言うのは、複素関数論でより明確になるのです。そもそも、実数を引数に取る関数は、
「複素数の立場から言えば、Im ( z ) = 0 の直線上で起こっている事に過ぎない」
のです。
フーリエ級数については、内積のところでもちょこっと触れましたが、もう少ししっかり述べると、
周期 2πの周期関数 f ( t ) とすると、n を自然数として、
f ( t ) ~ ( Ao / 2 ) + Σ[1;∞] { An cos ( nt ) + Bn sin ( nt ) }
でした。ここで、( Ao / 2 ) は
Ao = ( 1 /π)∫[ -π;π] f ( t ) dt
であり、これは例えば、f ( t ) という電気信号があったとすると、
「その電気信号の直流成分」
を示しています。
An, Bn は、級数の式の両辺に、cos ( nt ), sin ( nt ) を乗じて積分して得られるフーリエ係数です。これもやはり、関数列 { 1, cos t, sin t, cos 2t, sin 2t,・・・, cos nt, sin nt,・・・} が直交系をなしていて、
∫[ -π;π] cos ( nt ) sin ( mt ) dt = 0
∫[ -π;π] cos ( nt ) cos ( mt ) dt = πδmn
∫[ -π;π] sin ( nt ) sin ( mt ) dt = πδmn
となることを利用しています。(δmn は、クロネッカのデルタ)。そしてこれらは、周期関数 f ( t ) の波形成分の
「各周波数の正弦波成分の振幅」
「偶関数、奇関数成分の強さ」
を表しています。
ちなみに、一番長い周期の成分(この場合は 2π)がこの関数の周期を決めることになり、それを「基本周期」と言いますね。音で言えば、この周期が音程を決めるわけです。
さて、上のフーリエ級数は cos と sin があるので、虚数単位 j を導入して、
f ( t ) ~ Σ[ -∞;∞] { Cn e^( jnt ) }
と書けます。導出は簡単ですが、一応しておくと、「 Euler の公式」
e^( jnt ) = cos ( nt ) + j sin ( nt ) より、
cos nt = ( 1 / 2 ) { e^( jnt ) + e^( - jnt ) }, sin nt = { 1 / ( 2 j ) } { e^( jnt ) + e^( - jnt ) }
これを級数の式に代入すると、
( Ao / 2 ) + Σ[ 1 ;∞] { An cos ( nt ) + Bn sin ( nt ) } =
( Ao / 2 ) + Σ[ 1 ;∞] { { ( An - Bn j ) / 2 } e^( jnt ) } + Σ[ 1 ;∞] { [ ( An + Bn j ) / 2 ] e^( -j nt ) }
ここで、e^( - jnt) = e^{ j( -n ) t } と考えて、n を整数へと拡張すると、
Σ[ 1 ;∞] { e^( - jnt ) } = Σ[ -∞; -1 ] { e^( jnt ) }
とできて、改めて定数部分を Cn と置いてΣを結合すると良いわけです。
この表示で何が良いかと言うと、フーリエ係数を求めるのに、
Cn = ( 1 / 2π)∫[ -π;π] f ( t ) e^( - jnt ) dt
で済んでしまう事です。そしてなにより、
「級数{ e^( jnt ) }」⇔「係数{ e^( - jnt ) }」
の関係が見て取れるようにもなりました。さらにこれはもっと重要な拡張、ここのテーマである「ラプラス変換」の話へとつながって行きます。
それでは、フーリエ級数をいろいろな関数に適用する為に、拡張して行くことにしましょう。
まずは、周期を 2πに限らず任意の周期を取れるように、例えば、周期 T の関数
f ( t + T ) = f ( t )
に対して、
t → ( 2π/ T ) t'
のように変数変換します。すると、
t' : 0 → T
t : 0 → 2π
となり、周期 2πの関数と同じ扱い方ができるようになります。
さて、この ( 2π/ T ) は円運動で言う「角速度」、または振動で言う「角振動数」に他ならないので、
n ( 2π/ T ) ≡ n⊿ω ≡ ωn
と置くことにすると、フーリエ級数の式は、
f ( t ) ~ Σ[ -∞;∞] { Cn e^( jωn t) }
ここで、フーリエ係数 Cn は、
「角振動数ωn の関数」
と考えることが出来て、
Cn ≡ C ( ωn ) = ( 1 / T )∫[ -( T / 2 ); ( T / 2 ) ] f ( t ) e^( - jωn t ) dt
となります。( t は積分変数になっているので、結果残る変数はωn だけですね。)
ここまでは周期関数のフーリエ級数展開に限っての話でしたが、周期的でない関数も数多くあるわけで、こうした関数もなんとかこの方法で扱えないかと思うわけです。そこで、
「もしも周期的でない関数 f ( t ) がフーリエ級数展開できるとするならば、それは
T → ∞
と考えよう」
という話になったわけです。
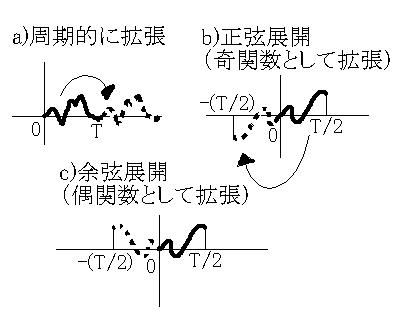
フーリエ解析では、
「関数 f ( t ) ( 0 ≦ t ≦ T ) を、f ( t + T ) = f ( t ) によって周期的に拡張」とか、
「 sin 展開、cos 展開」
というのが出てきますが、全ては「有界な区間で定義された関数」を、
「どう”周期関数の一部”とみなすか」
「いかにシンプルな形で展開するか」
という話なのです。(下図)
T を大きくすると言うことは、⊿ωが小さくなります。と言うことは、n によるωn の変化は微小になります。すなわち、
「 T →∞の極限で、級数は連続的に変化するωn について和をとる」
事になります。これは「積分」に他ならず、このときの C (ωn ) を C ' (ω) と書けば、
f ( t ) ~ ∫[ -∞;∞] C ' (ω) e^( jωt ) dω
もう少しちゃんと述べると、(これは数学的な式の変形なので、何がポイントになっているかをよく自分で追っていって下さい)
f ~ (ωn ) ≡ T C (ωn ) = ∫[ -( T / 2 ); ( T / 2 ) ] f ( t ) e^( - jωnt ) dt
とおいて、これを f ( t ) のフーリエ級数の式に代入すると、
f ( t ) ~ ( 1 / T )Σ[ -∞;∞] { f ~ (ωn ) e^( jωnt) }
ここで、
⊿ω = 2π/ T
であり、
1 / T = ⊿ω / 2π
と考えると、f ( t ) のフーリエ級数は、
f ( t ) ~ ( 1 / 2π)Σ[ -∞;∞] { f ~ (ωn ) e^( jωn t) }⊿ω
こう書けば、これは積分で言うところの「リーマン和」に他ならず、T →∞ のとき ⊿ω→ dω で、
f ( t ) ~ ( 1 / 2π)∫[ -∞;∞] f ~ (ω) e^( jωt) dω
と、積分の形に書けるわけです。
何がやりたかったのかというと、数学によく出てくる話として、
「何かの計算を極限に持って行く時はだいたい微積分が絡んでくる」
わけで、この場合、
「和を取る間隔を無限小にしていきたい」ので、
「なんとか”積分の定義式”まで持ってきた」
ということです。これも実は、内積のところでやった話と同じです。このとき、
f ( t ) ~ ( 1 / 2π)∫[ -∞;∞] f ~ (ω) e^( jωt) dω
を「フーリエ積分 ( Fourier integration )」と言い、
f ~ (ω) = ∫[ -∞;∞] f ( t ) e^( - jωt ) dt
を「 f ( t ) のフーリエ変換 ( Fourier transform )」と言います。
f ~ (ω) が、その関数の含んでいる振動成分(つまりフーリエ級数展開した時の正弦波)の周波数ごとの振幅(強さ)を表していていて、「スペクトル ( spectrum )」と呼ぶ、云々の話は教科書に書いてある通りです。
ちなみに、f ~ (ω) と書いたのは、これが f ( t ) の周波数領域の関数と見る事ができるからです。たまにこれを、
f ~ ( k ) = ∫[ -∞;∞] f ( x ) e^( - jωx ) dx
という書き方をして、「 f ~ ( k ) は f ( x ) の波数空間の関数」という表現をする人がいますが、これは波動関数を考えてみればわかることで、一次元の一般の波の式は、角波数 k 、各周波数ω、初期位相をφとすると、
u ( x, t ) = f { ( k x - ωt ) + φ}
と表されます。ここで x を固定して t の関数と見れば、
u ( t ) = f x { ( ωt ) + φ}
逆に、t を固定して x の関数と見れば、
u ( x ) = f t { ( k x ) + φ}
このとき、周期を T、波長をλとすると、
u ( t + T ) = u ( t ), u ( x +λ) = u ( x )
つまり、
「波の横軸を空間にとるか、時間にとるか」
の話に過ぎないという事がわかったかと思います。おまけとして、時間と空間の定数の対応を表にしておきます。
| 時間領域 t | 空間 x |
| 周期 T = 1/ν= 2π/ω | 波長 λ |
| 周波数ν | 波数κ |
| 角振動数ω | 角波数 k |
f ~ (ω) = ∫[ -∞;∞] f ( t ) e^( - jωt ) dt
の「無限積分」が収束すれば良いわけです。
ここで、上の積分を
f ( t ) と e^( - jωt ) の「内積」
と見ることが出来るので、それを使ってこの値の最大値を考えていくと、
| f ~ (ω) | = |∫[ -∞;∞] f ( t ) e^( - jωt ) dt | =
|| f ( t ) || || e^( - jωt ) || | cosθ| ≦ || f ( t ) || || e^( - jωt ) ||
ところで、ここで注意しなければならないのは、
e^( - jωt )は「周期関数」
という事です。指数が実数の時は発散、又は収束しますが、虚数の時は
「複素平面上での回転」
になるのです。よって、この最大値を A とでもおけば、
|| f ( t ) || || e^( - jωt ) || ≦ A || f ( t ) ||
ということは、フーリエ変換が存在するには、
「f ( t ) の定義域無限大でのノルムが有限」
であればよいという事になります。さらに「三角不等式」を使えば、
|| f ( t ) || = {∫[ -∞;∞] { f ( t ) }^2 dt }^(1/2) ≦∫[ -∞;∞] | f ( t ) | dt
となります(要するに、「コーシー・シュワルツの不等式」)。一番右の積分を「絶対積分」と言い、この絶対積分が収束すれば、フーリエ変換が存在するのです。
ちょっとこの意味を直観的に考えてみましょう。| f ( t ) | の積分値を考えると言うことは、戻り値が常に正となる関数 f ( t ) を考えれば十分です。この積分が無限大の領域で収束するにはどうすれば良いでしょうか。
例えば、f ( t ) = t^2 などの下図の( a )のようなは明らかに収束しませんね。また、( b ) の関数は戻り値は収束していますが、無限大に行くにしたがってスプレーをかけた部分の面積は増えて行きます。
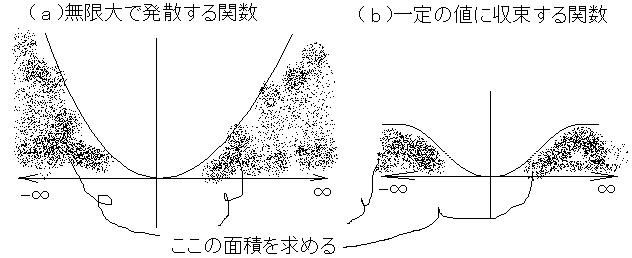
では、どのような関数なら収束するかというと、要するに下の図( c )のように、∞の「両端」で、積分領域が「閉じている」関数なら収束すると言えます。
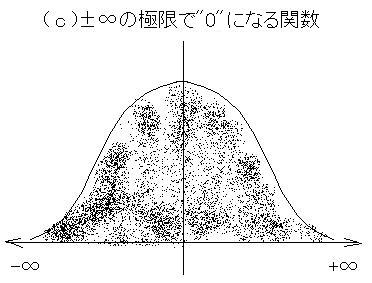
数式で表すと、
lim[|t|→∞] f ( t ) = 0
という事になります。これを、「絶対収束」と言い、フーリエ変換が存在する「必要条件」は、「関数 f ( t ) が絶対収束する事」となります。
a ) u ( t ) = 1 ( 0≦t ), 0 ( t<0 )
b ) r ( t ) = t ( 0≦t ) ,0 ( t<0 )
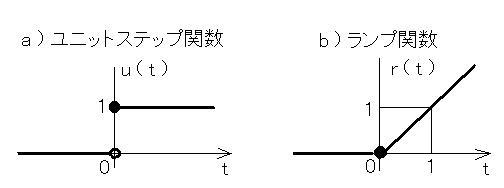
などです。( a ) は、電気回路で言えば「直流電源の入力」にあたり、制御の分野では「ステップ入力」と呼ばれる、ごく日常的なものです。
しかし、前項の条件ではこの「絶対積分」は発散してしまいます。そこで、ある「良い関数"Φ"」を使って、これを収束させようと考えたわけです。すなわち、| t |→∞の極限で"0"に収束しない関数
lim[|t|→∞] | f ( t ) | ≧ C
に対して、f ( t )Φ( t ) を作り、
lim[|t|→∞] f ( t )Φ( t ) = 0
「良い関数」とは、| t |→∞の極限で、「何度も微分」でき、任意の「多項式関数の逆数」よりも「速く"0"に収束」する関数を言います。任意の多項式と言うと、単純に以下のようなものが考えられます。
a0 + a1 t + a2 t^2 + a3 t^3 + ・・・
ここで思い出して欲しいのが、「マクローリン展開」です。上の式で無限級数をとれば、すなわちこれは、
A e^( at )
と言う形に近づいてゆくでしょう。この「逆数」が、上の「多項式関数の逆数」よりも速く"0"に収束するのですから、つまり、「指数関数 e^( -σ| t |) (σはある正数)」を「良い関数」として、
f ( t ) e^( -σ| t |)
を作れば、このフーリエ変換は存在します。
こうして、「"0"に収束する関数」をつくって「フーリエ変換」をしたのが、「ラプラス変換」と言えるのです。式で書けば、
L{ f ( t ) }≡F ( t ) (ラプラス変換)
= F{ f ( t ) e^( -σ| t |) } (フーリエ変換)
= ∫[ -∞;∞] f ( t ) e^( -σ| t |) e^( - jωt ) dt
= ∫[ -∞; 0] f ( t ) e^(σt ) e^( - jωt ) dt +∫[ 0;∞] f ( t ) e^( -σt ) e^( - jωt ) dt
s≡σ+ jωとおけば、
L{ f ( t ) } = ∫[ -∞; 0] f ( t ) e^( s~t ) dt + ∫[ 0;∞] f ( t ) e^( -st ) dt
s~ = σ- jω(共役複素数)
と、ラプラス変換の定義式になります。